The Desmos Art Project

In the last week of two of school, the 8th graders worked on Desmos art projects. It is a glorious capstone to their K-8 math experience at our school. The classroom teacher had given some loose constraints — use at least 8 linear equations, use at least 4 inequalities, use at least 4 horizontal lines, etc. — and then breadcrumbed different techniques over the course of the week. She gave them formulas to help create unfamiliar figures, like circles and ellipses. The next day, she taught them how to create a custom color. Then, after students had mucked about with inequalities for a few days, she introduced the polygon tool as an inefficient way to color in areas. (Outline a set of points, and the Desmos graphing calculator will shade the interior!)

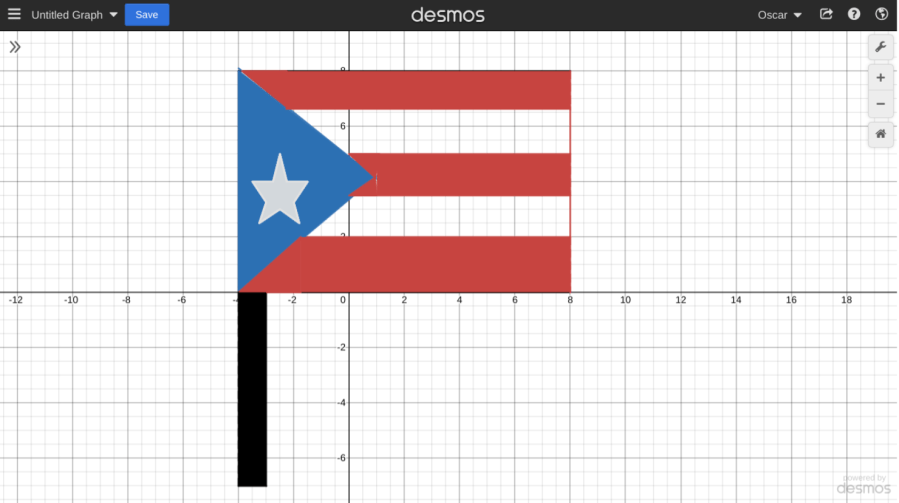
Within a few days, graphs were shaping into true artwork. Sebastian had designed a Puerto Rican flag to honor his heritage. Nora had been wrestling with her feelings around the transition from our little K-8 school to the town’s only high school, and so she was working on a nostalgic rendition of the PBS Kids logo, a fixture of her youth.

I ran into Catalina in the hallway. “Ms. Laib!!! I miss working with you!” Last year, she was in a section of 7th grade that I co-taught, and I saw her in a small group for part of the school year.

“Aww, I miss working with you, too!” I gushed. And I do. I’ve known her for years, and I’m enormously proud of her mathematical journey. She now advocates for support when she’s feeling confused. She demonstrates agency in class. She had an impressively high growth score on last year’s state test. This girl is primed for high school.

“Do you think…” she paused, and then started again with lowered voice. “…that you could help me with my Desmos art project? It’s due soon and it’s really hard.”

We cheerfully arranged to meet later that day.

Reviewing Catalina’s Work

Catalina pulled out her initial sketch that she had made on grid paper. Then she opened her chromebook slowly, turning it to face me. She offered an apologetic smile.

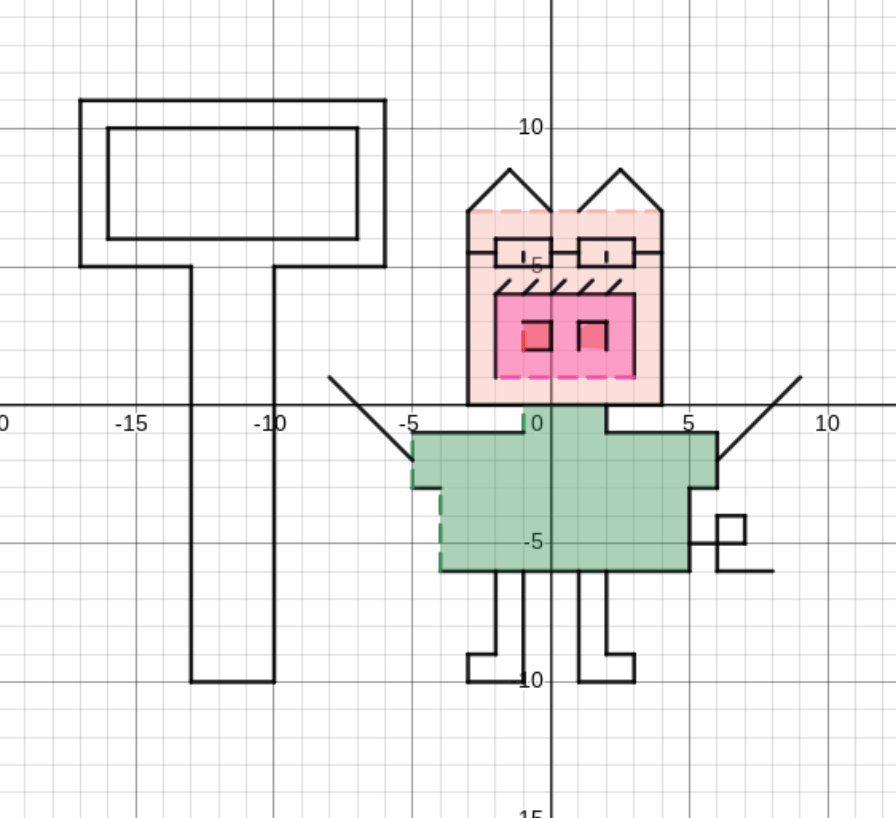
Catalina had created a lopsided cat. Its ears floated just North and East of its wide, oval face. Its whiskers were charmingly askew. For all of his asymmetries, this cat represented a lot of mathematical prowess.

“Hey! It’s cute!” I smiled, genuinely.

“Okay, but I have a lot to do, and I don’t know how to do the mouth at all!” She pointed to the parabola of its tiny feline lips.

“Okay, let’s start slow and then go fast. How did you come up with the equation for the ellipse?” I asked her.

She pointed to the paper with the assignment. “I just replaced the h and the k and the a and the b with numbers.”

Catalina had written:

“Okay, and then how did you come up with the whiskers?”

“I had already drawn my cat on paper.” Catalina pointed again to her sketch. So I figured out the slope of the lines using slope triangles and, you now, rise over run.” Yes! There was so much from here! I had her show me how she determined the linear equations to use. “But because the cat’s head isn’t where it should be, like in my drawing, none of the whiskers really make sense.” She looked up at me with big, saucer eyes. “This is frustrating.”

“It sounds like every time you go to add something to. your cat, you have to figure out an entirely new equation. That is frustrating.”

Her eyes slanted downward. “So… there’s another way?”

Another Way

“Okay, you see how in your drawing the cat’s face is centered? Along this line… do you remember what it’s called?”

“The y-axis?”

“Yes! And it’s symmetrical across that line.”

“Yeah, it made it easier for me to draw, because I could make it mirror image.”

“Well, I have some good news: the mathematical equations might be easier to figure out when it’s centered, because you’ll notice some connections. The bad news, though…”

I saw the muscles around Catalina’s eyebrows tense. “Please. Please don’t make me start over.”

“I think you’re going to like what we’re about to do…”

“But it’s due on Friday! Please! I can’t start over!”

I saved her work, and then shared it to another tab.

“It’s okay. We’ll save your work, and make a second version. You can continue with whichever cat you prefer.”

Her face relaxed, ever so slightly. “Okay.”

A Brave New Ellipse

We started with an ellipse. I recorded the equation in the graph.

“I’m going. to add sliders for the values. of and , I said, narrating each move. “Play around with . What happens when you change the value? Can you get it to be centered along. the y-axis?”

It didn’t take long for Catalina to discover that a value of 0 centered her new ellipse. “Oh, that makes sense, because it moves side to side, along the x-axis. But I don’t want it to go side to side. I want it to the middle.”

Catalina had never studied equations for circles or ellipses in class, but she was starting to figure out how how the parts of the equation work. It’s like she’s diagramming a mathematical sentence.

She moved onto . “I got it!” She exclaimed. And then she looked at her sketch. “Oh, okay, so my middle of my oval was the and. it turns out is and is . That can’t a coincidence, right.”

I smiled — perhaps smugly, because Catalina responded with, “you’re so sneaky, Ms. Laib!”

A Colorful Cat

Catalina had recorded an equation.

“It’s still going to take us forever,” Catalina lamented. “And everyone else in my class has shapes colored in by now.”

“Okay, so. let’s color in your cat! So the red outline of his face is because every point along that rim is a solution to your equation.”

“It is?”

“Yeah, so if you put it a value of for and for , you land here on the far right edge. Trace it. All of those points are solutions.”

“So how does that help me color in the face.”

“Well, we want something that’s going to color in all the points on the inside, too.”

“Yeah, I don’t know what you’re talking about, Ms. Laib.” Catalina glanced towards the door, perhaps plotting her exit.

“Okay, so let’s pick a point on the inside. Like this one. . These two values are either going to result in something that’s too large or too small for for our equation that equals 1. If it’s too small, we can use a symbol that looks like…”

“Oh, the alligator!” Catalina exclaimed.

“Also known as greater than or…”

“Less than! So, wait, where does it go?”

“Well, if the values are too small, it’s not going to be equal, it’s going to be…”

Catalina grabbed the computer, and replaced the equal sign.

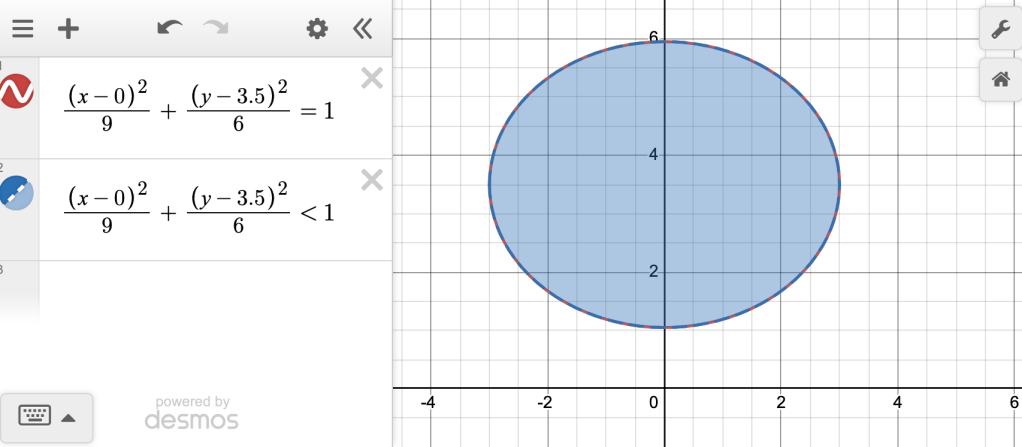
“We could also use the symbol for less than or equal to, which would capture all the points along the rim and also all the points on the inside.”

“Um, Ms. Laib, let’s focus on the ears.”

Opposite Slopes

Catalina used her sketch to figure out the equations for the downward slope of the left ear. “Okay, so it’s going down 3 every time it goes over 2, so it has a slope of . She wrote .

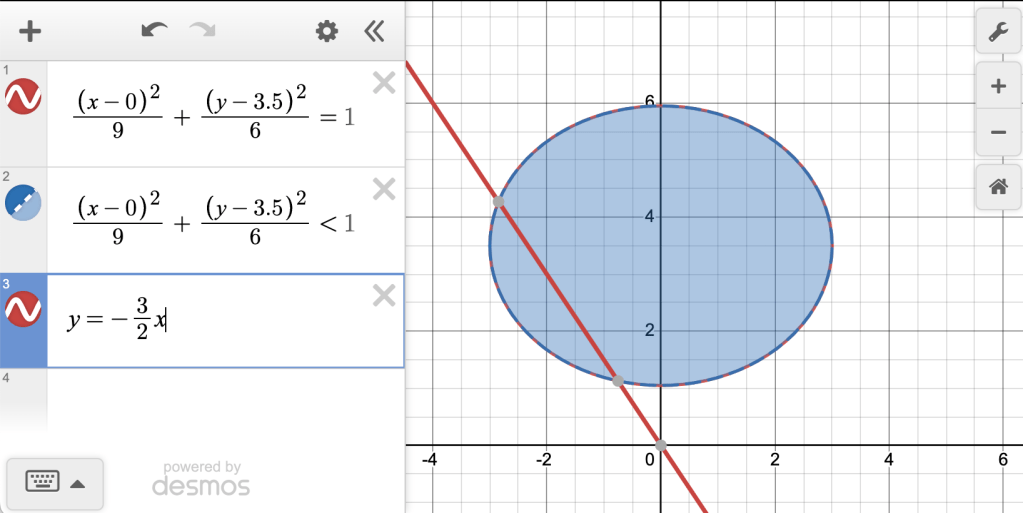
“It looks like it’s. in the wrong place,” Catalina lamented. “Why is it so far down?”

“Okay, so it looks like you’re writing your equation in slope-intercept form,” I told her. She looked at me blankly. “We often write it as

“Ohhhh, and the ! That’s the y-intercept. I’m guessing it needs to be, like… five. From my drawing.” She adjusted the equation to . and breathed a sigh of relief.

“But I want it to not go all the way across,” Catalina started.

“Oh, totally, and we will fix that in a minute. But first, do you see the other ear? Is there part of it that reminds you of the line that we just did?”

Catalina bit her bottom lip, and then pointed to the reflected line. “Yeah, it looks like a mirror image! Okay, so if before it was , now it’s going to flip like a mirror. .” Catalina typed in the equation and let out an exasperated UGH when she saw the result.

“It’s okay! Let’s slow down again. So the two equations you just wrote both have negative slopes.”

With a heavy breath, Catalina added, “yeah.” I waited. It felt like an eternity.” “Oh, they’re both going down!” She finally said. “And I want the other one to go up! So it has to be positive!”

“Precisely! Go back to your original equation and try that.”

Catalina typed in . “Ohmygod, this isn’t so bad!” She pumped her fist once.

“It’s really not! Now let’s figure out how to make the lines into line segments. Point out the part that you want to be included,” I directed. Catalina pointed to the intersection of the red line and the ellipse of the face. “Okay, so what’s the biggest value you want for x?”

“I don’t know… ?” Catalina asked.

“Exactly. So x needs to be less than that.” I showed her how to restrict the range with .

“Okay, so how far should the line go? What’s the lowest value of that you’d want?”

“I don’t know… 2? 2.5?”

We wrote it in.

“And now, for the other ear?” I showed Catalina how the reflected lines actually intersected with the ellipse at…”

“More opposites!” said Catalina, ducking her head to hide any traces of excitement. There were other people around, after all. “So it’s going to be the opposite. It’ll be .”

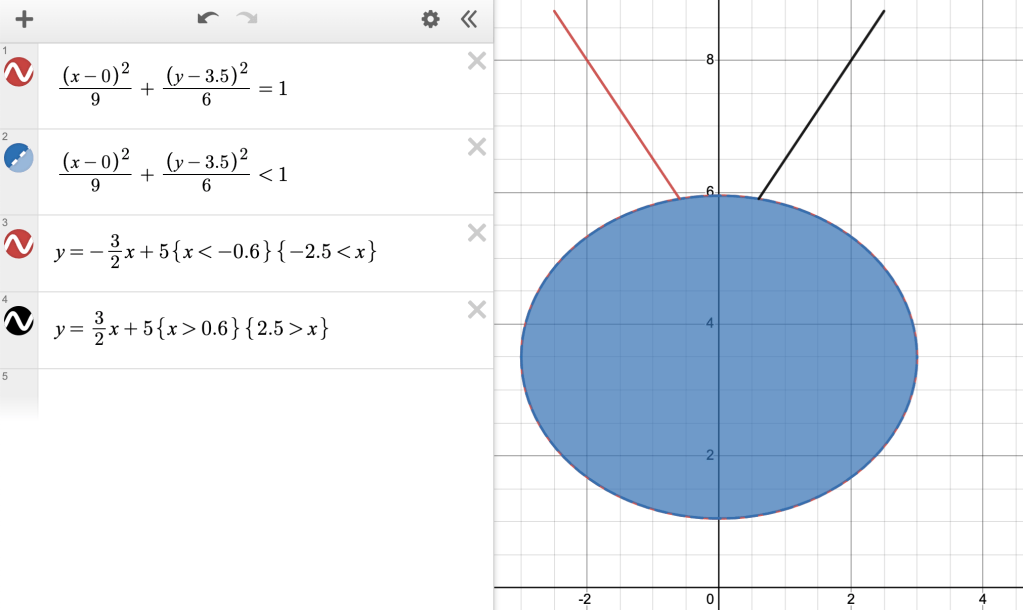
This cat was shaping up.

Finishing the Cat

“Let’s look for more opportunities to use opposites. We’ll have to think about how to deal with the reflections. Will the slope change? Will the inequalities change? How will they change?”

Catalina confessed that she had spent a whole class period on the crooked whiskers “that look hideous, right?” she asked.

“Well, they’re not symmetric, if that’s what you mean,” I confessed.

It took only a few minutes to make our new whiskers. She came up with the equation for one downward sloping whisker, and then translated it. Use a different chunk. Change the y-intercept slightly. Use the opposite slope for a reflection across .

Eventually, Catalina had created a remarkably elegant little cat.

“He looks like a little like Pete the Cat,” I said. “Only very dapper.”

“Dapper…” Catalina trailed off for a moment. “Isn’t Dapper Cats a thing?”

“Oh, it’s a Desmos thing!” I told her. “There’s a lesson about dapper cats! I can’t believe you remember that!”

“Yes! of course I remember it!”

Catalina’s dapper cat looks particularly aloof, but, hey, she needed to include at least four horizontal lines, and those were easy ways to get them in.

“So were you okay that we started over again?” I asked Catalina.

“Oh, yeah, it was so much better when we could just change the slopes from positive to negative and negative to positive.”

Goals for Catalina

Catalina was working towards a product, but I had other goals in mind during our two sessions together.

• Determine the slope of lines using two points on the line. (from her sketch)
• Understand the meaning of each variable in an equation written in slope-intercept form ().
• Use an understanding of ‘opposites’ to reflect work across the y- or x-axis.

There are lots of other goals we could have had when working on this project. For example, we also worked on restricting the range of a line using intersecting points and solutions. When conferring with other students, we talked more about parallel lines. For others, we solved systems of equations to determine points of intersection. However, it felt more important to me that Catalina focus on really understanding slope-intercept form, and playing around with different elements of linear functions.

A few days later, Catalina submitted her final project, which included a written reflection.

Describe any changes that you made from your original design on paper. Is there any reason why your Desmos art does not exactly match what you originally drew on paper?

I made a the mouth just straight, not curved, because I thought it would be easier to do. I also changed the design by adding a bow to the cat. I made the cat wear a bow because i needed to have more diagonal lines and i found out it was pretty easy to do.

She added:

I think my inspiration to make the cat was from the one lesson we did on desmos about dapper cats that made me remember that they don’t have to be hard to draw and i can change the size of anything.

She also expressed a few things she wish she could have changed — the overlapping shaded areas, for example — but that ultimately she’s proud of her work.

I feel very proud that I got this done with in only a couple of days. Seeing all the drawings from last year’s class was a little overwhelming, because they were so good, but now I see that it wasn’t impossible. You just need to be patient with yourself.

Words to live by!

On the last day of school, Catalina and a few other eighth graders dropped by my office to chat. We reminisced about our last few years together, over muffins and some stolen orange juice from the teachers lounge. Every year I say goodbye to another 8th grade class, and every year I miss them. I’m just a sentimental fool.

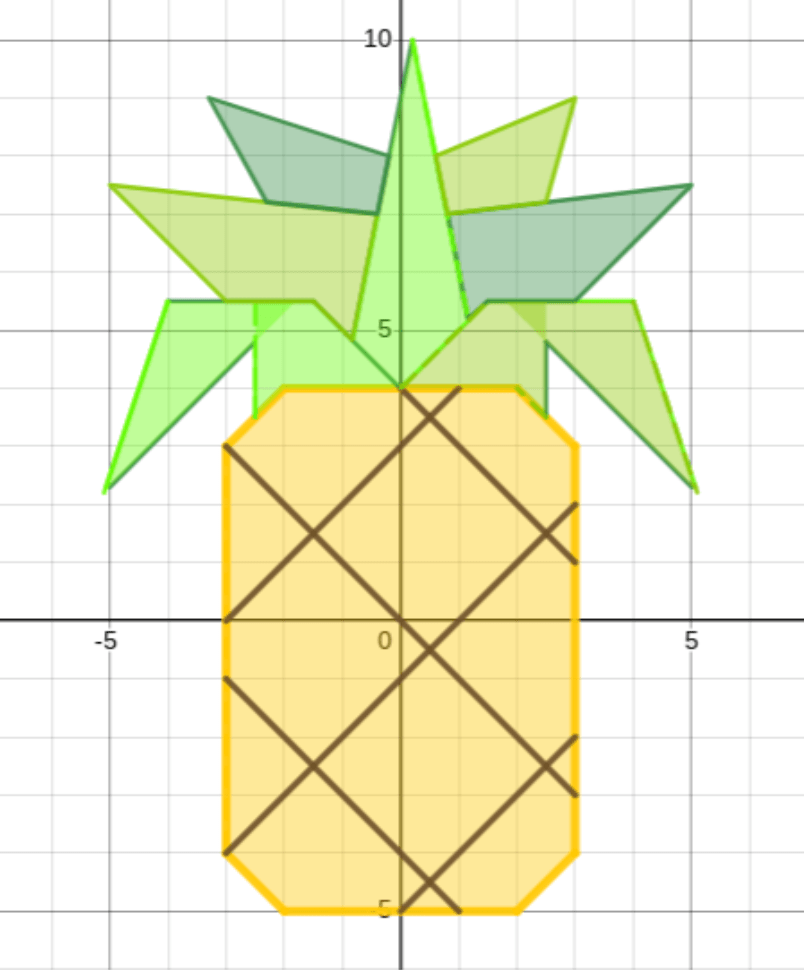
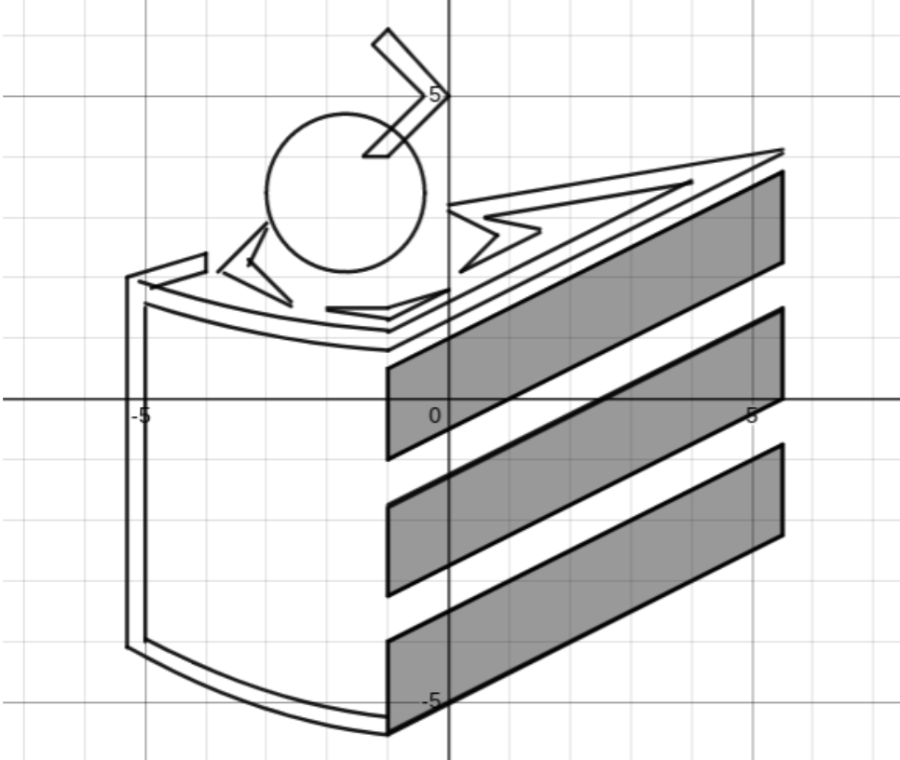
Sample Projects

Here is Catalina’s finished project, with all the equations. And here is a slideshow with a few other 8th grade artworks.

I love that this project had so many different entry points for students, and that the long work periods allowed us to confer with students in a more meaningful way. Using a visual platform like the Desmos graphing calculator meant that students got immediate feedback about the accuracy for their lines, and also afforded opportunities to play around with different values and elements within the equation. I can’t think of a better way to synthesize and simultaneously build on all of the 8th grade work with linear relationships and equations.

And it allowed for self expression. One group of girls all created different Peppa Pig family members. Several kids created flags of countries, territories, and Champions League football teams. Some of these students have been in our K-8 school for nine whole years. They’re about to enter a much larger high school, pulling from every school across town, and they’ll need to find their place. They will question their own identity. I hope they find things to ground them.