Exploring Geometry with Simon Gregg (Addendum to ‘Digging in the closet’)

Shortly after posting my recent blog post — “Digging in the Closet: The Return of the Museum of Rarely Used Math Manipulatives (MoRUMM)” — I received a DM from Simon Gregg (@simon_gregg). Simon is a primary teacher in Toulouse (France) who offers brilliant insights into teaching, learning, and mathematics, with his trademark brand of humility and curiosity. He respects the humanity of even the smallest children in his charge, and treats the mathematics at a pre-kindergarten level just as seriously as he does the mathematics of high school algebra. (As you may have guessed, he is a hero to me. If my opinion holds any weight at all, you will immediately leave this post to consume his blog, or one of his books, and then follow him on twitter.)

So I was thrilled to receive a DM from him. The message arrived as I was leaving work to pick up my children.

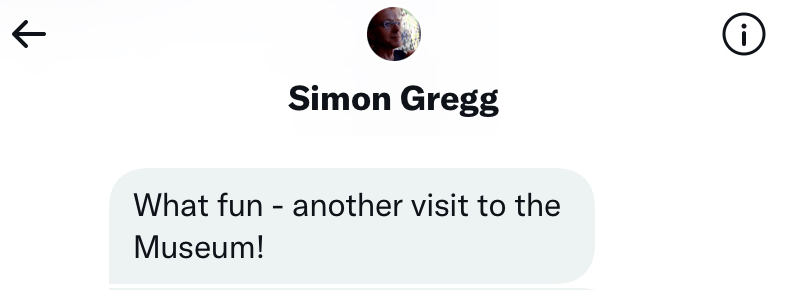
My cheeks grew red and warm, swelling with pride at the acknowledgment. then, Simon continued:

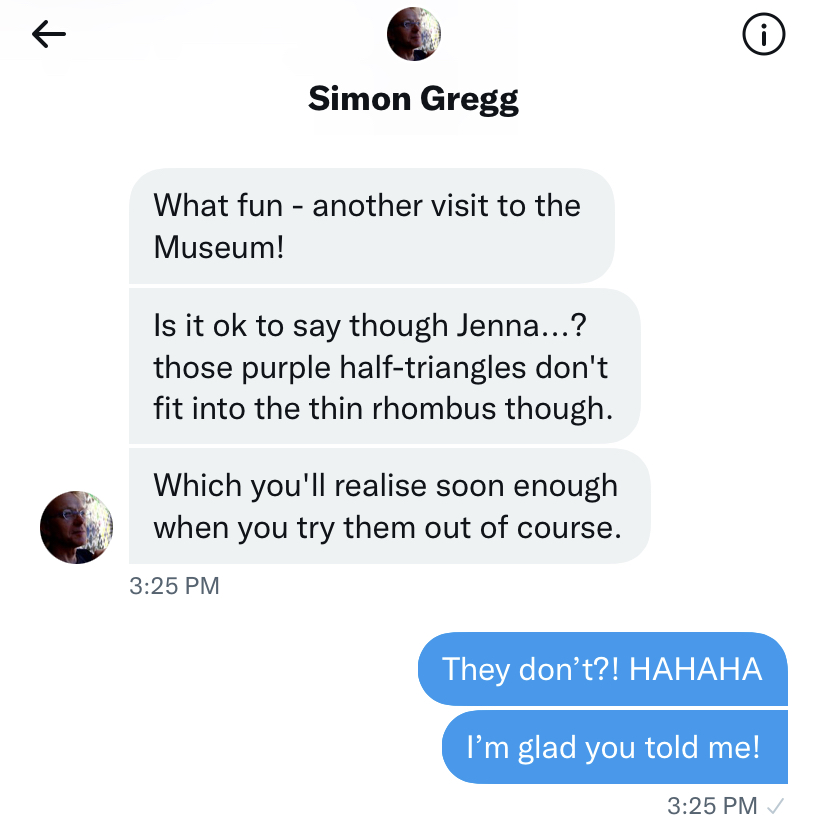
I burst out laughing!

Like I could have easily become a ‘spit take’ meme, if anyone had a camera trained on the staff parking lot.

Of course! I had just posted an entire blog post all about the purple half-triangles, and, hey, it was mathematically unsound. I didn’t feel any embarrassment over it. Simon is one of the most passionate learners that I know, and the ideal learning partner!

Our conversation continued.

The Dilemma

To recap the last blog post: my students had been filling this ‘dog’ outline with pattern blocks, trying to figure out strategies for using as many blocks as possible. I thought that we had created the maximized design here, when one student said… what if we traded those thin rhombuses for 2 triangles? After all, we had traded one (thicker) blue rhombus for 2 green triangles.

Students agreed that these new triangles did not look like the green triangles. They were too pointy. Too skinny. That’s when I remembered that I have thinner purple triangles, representing 1/12 of a yellow hexagon, hidden deep in a closet. These students had inadvertently invented a need for these 1/12 triangles!

…or so I thought. 😂

Simon’s Evidence

“[The purple triangles] are right angle triangles. that half-tan rhombus is isosceles,” Simon continued. I didn’t have the photo of the purple triangles handy, but I thought about it.

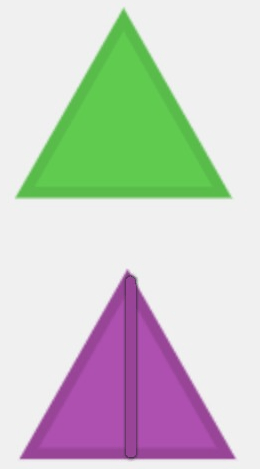
Oh, of course! Splitting that triangle down the middle forms a perpendicular line, and angles measuring 90°. It all felt so blazingly clear. I couldn’t help but giggle as I took the final steps to my car. In the student work sample, we had split the tan rhombus across the thinnest part of the shape, which actually formed a diagonal, not a perpendicular bisector.

Simon’s proof was so elegant. Meanwhile, while reasoning through that blog post last night, I had used a different line of thinking.

Proving Congruence… or not

I did not have any purple triangles handy while writing that blog post. Instead, I had designed the images above, based off an image I have of the physical pattern blocks.

Ah, yes, confirmed: two purple triangles match one green triangle. The area of the purple triangle is 1/2 the area of the green triangle.

First, I thought about side lengths.

i know that pattern blocks are based off a side of 1 inch. All six sides of the hexagon are each 1 inch. Likewise, of the sides of the blue rhombus, the green triangle, the orange square, and the thin tan rhombus are all one inch. That means that a side of the purple triangle is also 1 inch, as it matches the green triangle.

Then I thought about the angles involved in the tan rhombus. Placing two of the ‘pointier’ sides together will form the same angle measurement as the green triangle.

The green triangle is equilateral, and thus all of the angle measurements are 60°.

Which means that the pointy side of the tan rhombus has an angle measurement of 30°, which is the same as that vertex of the purple triangle. Yes! I was onto something!

Quickly, I thought about what that means for the remaining angle in the tan rhombus. The smaller angle measurement and the larger one are supplementary, meaning that they sum to 180°. That means that the larger angle on the tan rhombus measures 150°. That looked to be about right… (but irrelevant, haha.)

So I had proved a congruent side and an adjacent congruent angle. I finished the blog post, and posted it.

But side-angle is not a congruence theorem, is it. In order to prove congruence, I would need to have more information.

Angle-Angle Similarity

In a triangle, knowing the measurement of two angles is enough to prove congruence. That’s because, with those two angles defined, the third angle is a given. The sum of the interior angles of a triangle is 180°, so the third angle would be 180° – measure of first angle – measure of second angle.

I had only thought about one angle. If i’d taken it one step further, I would have noticed that I could tell the measure of the other two angles. One of them wasn’t impacted by the slice in half, so it would remain 60°. That makes for angles of 30°, 60°, and 90°, while the half-tan rhombus is definitely isosceles, as Simon pointed out. (It’s also clear that the perpendicular bisector created a 90° angle, meaning that I could have used that in combination with the 30° angle to prove angle dissimilarity.)

I also knew that the obtuse angle in the tan rhombus is 150°. (The sum of the interior angles in a quadrilateral is 360°, and the rhombus is composed of pairs of congruent angles. Therefore, adjacent angles should be supplementary, and I can determine the measurement of the obtuse angle with 180° – 30°.) Slicing it in half yields an angle of 75°, which is not featured at all in the actual purple triangle.

Side-Angle-Side Theorem

If I had wanted to take into account that 1 inch measurement, I could have thought about how all of the sides of the tan rhombus are 1 inch long. Cutting it in half, across the shortest distance, preserves two 1-inch sides, joined at a 30° angle.

The 30° angle in the purple triangle is created by halving the 60° angle of the green triangle. However, the two sides on the green triangle are not both 1-inch sides. The perpendicular bisector is less than 1 inch. Therefore, while both a side and an adjacent angle are similar, the next side is not, so the two triangles are not congruent. Which brings me to…

Side-Side-Side Theorem

In my quick thinking, I was using the known side length of one inch for all of the shapes (green triangle, purple triangle, tan rhombus), and then a known side length of 1/2 inch as the base of the purple triangle (1 inch, cut in half). it seemed reasonable to think that the diagonal length from vertex to vertex and then an estimated side length of 1/2 inch going across. Sure! Looked good!

But, in thinking about the side measures of the actual purple triangle, we have a side length of 1 inch, a side length of 1/2 inch, and then a side length of decidedly not 1 inch. There is no way to cut through an equilateral triangle with side lengths of 1 inch and have the measurement inside the triangle also be 1 inch.

Simon’s Area Reasoning

“They’re also not the same area,” Simon shared via DM.

That makes sense. The two triangles aren’t congruent, for one, but also we can use the law of cosines.

Let’s have the angle I love so much — 30° — stand for c, and the two 75° angles act as a and b.

a^2 + b^2 – 2ab cos c

That gives me 75^2 + 75^2 – 2(75^2) cos 30° can simplify down to just cos 30°, which is √3/2, or approximately 0.86 inches. That side length at the bottom isn’t 1/2 inch at all. So the base is different, and while one side length is the same, the other is different. The odds of it being the same area? So small that I won’t even calculate it.

Learning From Mistakes

In summation: I am so glad that Simon contacted me! I was glad to think through some of the reasoning, and to have someone to share a few ideas. Simon is someone who is so thoughtful and genuine, that he was able to make me feel totally comfortable even when I had posted a long blog post hinging on a mathematical inaccuracy. We could laugh together.

The Beauty of a Messy Closet

My officemate rearranged a few things in the closet while I was teaching remotely last year, and I could not locate the purple triangles today.

I’m glad. It gave me the chance to work some of engage in more mathematical thinking! Otherwise, I might have just paired up the tan rhombus and the purple triangles, and quickly noticed, “oh, those don’t match.” Maybe I would have wanted to know why. Maybe I would have moved on.

But today, I had a good laugh and some geometric thinking. Just delightful.