It’s surreal to be back at my school, in person, after 18 months away. I feel a tremendous sense of vertigo when I look around at this place that is so familiar to me — a home way from home — and realize that it underwent all of these changes while I was gone.
To combat some disorientation, I visited a bunch of classrooms today. Among them was a sixth grade class.
I’ve known this particular cohort since they were in Kindergarten. (Here they are in first grade!) Several of them greeted me today warmly, their eyes crinkling to betray a smile even when their mask obscured their lips.
I joined a pair of boys — Oliver and Nico* — who were engaged in a lively debate about what a shape reminded them of.
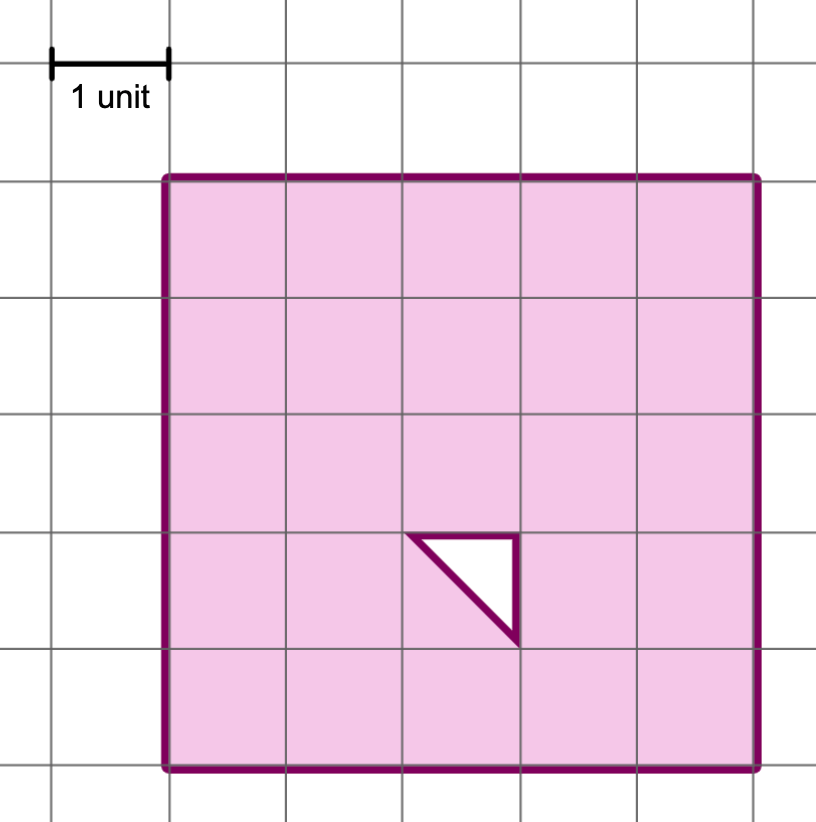
“It’s an angry cube!” Oliver chuckled.
Examining Oliver & Nico’s Work
At first glance, their papers looked very similar. They had painstakingly labeled each unit square, as if counting by ones.
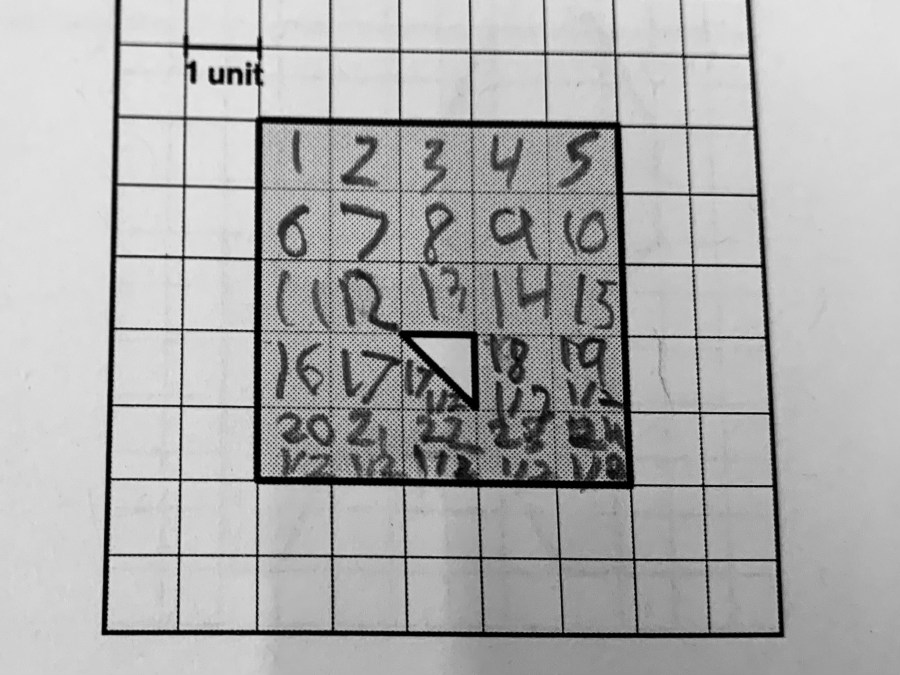

“Tell me about what you did here,” I started, only to be interrupted by Nico’s unbridled enthusiasm: “Look! I showed my work!”
Nico has known me for years. He knows that I love hearing about his thinking, and I love when students communicate it on the page. However, I wasn’t convinced that either one of them had truly counted the unit squares one by one.
“Did you count them all?”
“It was really hard to fit in there, with all the fractions!”
All the fractions? I looked closer at Nico’s work.

He had counted by 1s, up until he hit the half square. “1, 2, 3… 15, 16, 17, 17 1/2, 18 1/2, 19 1/2,” etc.
“So when you were figuring out the total area, which is…”
“24 and a half,” Nico beamed.
“Right. Twenty-four and a half. So did you count exactly as you showed here?”
“Well, no, this isn’t how I solved it. I was just showing my work!”
Meanwhile, Oliver had labeled the length and width on his (5) but then labeled each whole unit square, 1 through 24. He then labeled the 1/2 square, for a total of 24 1/2.

“And did you count by 1s, Oliver?” I asked.
“No, that’s just how I show my work! Isn’t it pretty?”
I nodded. I hope the boys could see my smile, too. I love the look of student mathematical thinking on the page, so, yes, definitely pretty. However, it didn’t accurately represent their strategies.
“So, if you didn’t count by ones…” I paused. “How did you figure out the total area?”

“I did five times five minus one-half,” Oliver stated cleanly. He wrote the equation down on his paper. Elegant.
“Oh! That seems more efficient!” I exclaimed.
“Yeah, but not as pretty!” Nico countered.
“Is it really showing your work if you did something totally different?” I asked.
“Well, I mean… I also counted by ones. Can’t you tell?”
Touché.
What does it mean to “show your work”?
Teachers use so many different phrases: show your work, make your thinking visible, justify your reasoning, etc. Basically: communicate your thinking! Help others get inside your mathematical ideas!
Maybe if we had told Nico and Oliver to “make their thinking visible” they would not have labored over a misrepresentation of their thinking. (Or maybe not. I don’t know!)
I very deliberately wrote “examining Oliver and Nico’s work” above, because I had to peel back a few layers, through oral questioning, in order to get at Oliver and Nico’s thinking.
There can be a fundamental disconnect between what many teachers intend and how students interpret the request to show their work/make their thinking visible/etc. I want to be able to understand the student’s reasoning! Meanwhile, the students want it to show some reasoning clearly, even if it’s not how they solved the problem. What are the students valuing when they do this?
How do we support students in valuing accurate communication over painstaking but pretty?
Student Agency
One thing we can do is anchor classroom discussions on student thinking and work samples. Please note that I do mean discussions — true discourse, and not just a “show and tell” of different, disconnected strategies.
When I do this, I orchestrate the classroom conversations using the five practices (anticipate, monitor, select, sequence, connect). Students drive the discourse, and demonstrate some agency, but I’ve engineered some of it behind the scenes. I’ve selected certain students in order to highlight specific mathematical ideas, and push thinking forward. It does not always work perfectly — obviously! I’ve known these boys for years, and yet…! However, over time, I think it shows that the value is on the thinking and not on the pretty product.
While recording student thinking during number talks and other discourse-based routines, I emphasize that I want to accurately represent their ideas. I frequently ask if the way that I recorded what they said matched their actual thinking. (And sometimes a student will quickly answer, “no! It doesn’t!”) This reinforces ways to show thinking, as well as the value of accurate depictions.
I’ve also tried to change the language I use from “show your work” to “make your thinking visible.” I think it might make a difference, although that’s my completely unscientific opinion.
I’d love to visit Nico and Oliver again later this week to see if this is something they do regularly.
*As always, all students are referred to by a pseudonym.
Discover more from Jenna Laib
Subscribe to get the latest posts sent to your email.

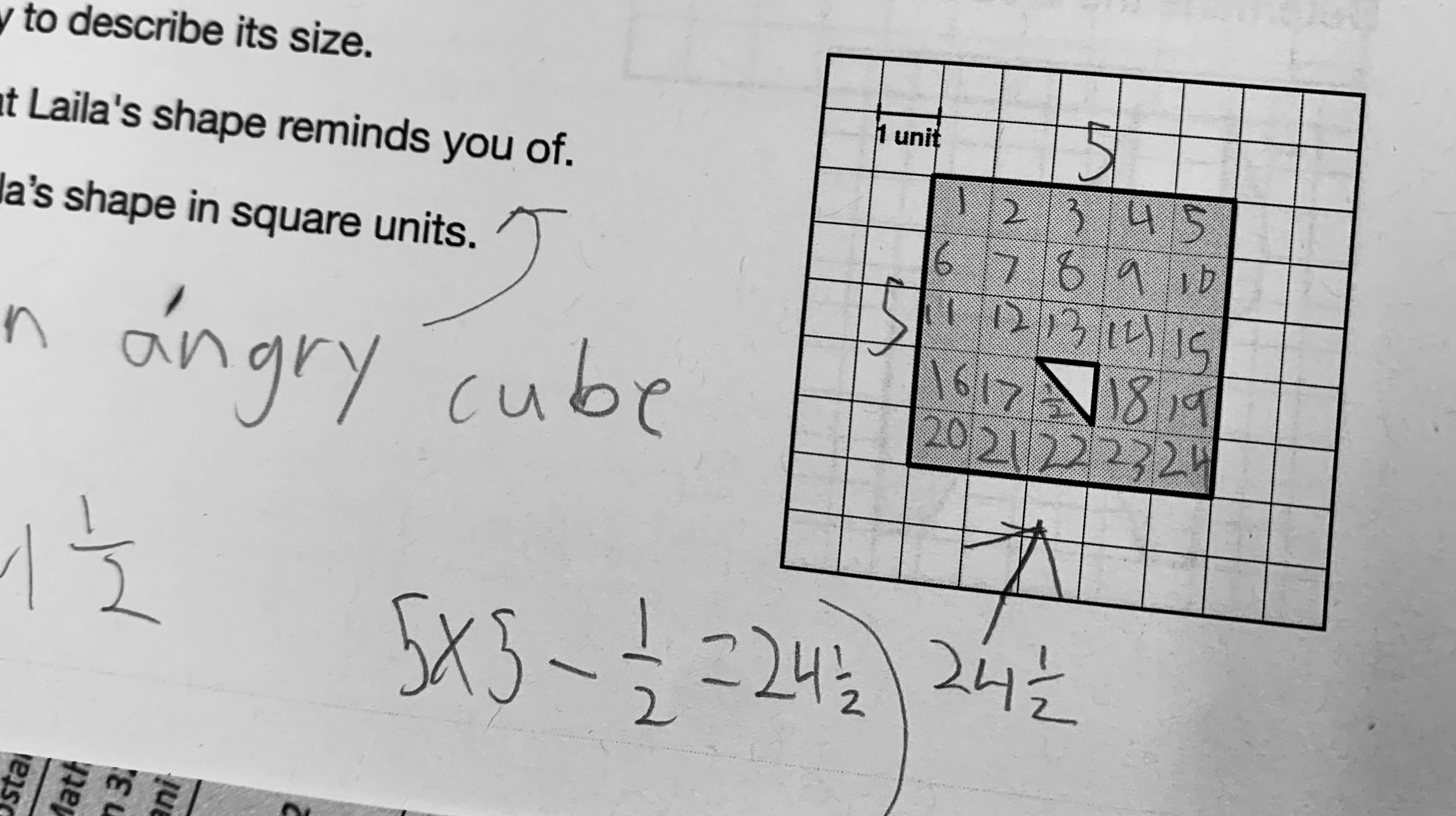
1 Comment